


If you plan to study art or archaeology to get away from math, think again.
But, it’ll be alright. You’ll be thinking mathematically and you won’t even know it.



Suppose an archaeologist brings you examples of designs that he found in an Egyptian village. In these designs, you have observed the following different transformations:
H − Horizontal Line Symmetry
V − Vertical Line Symmetry
R − Rotational Symmetry of 180° (or Point Symmetry)
and T − Translational Symmetry.
Any design that you observe may have zero, one, two, three, or all four of these symmetries in one design.
1) Using just these four symmetries, how many different possible combinations are there?
2) List all of these possibilities.
However, when the archaeologist brings you the different examples, he only brings you the 12 designs on the next page.
“Wait,” you say, “I’ve listed more possibilities than what you’ve brought me.”
Then you realize, some of the possibilities aren’t possible by themselves. For example, there is no possible design for HV, horizontal and vertical line symmetry. Realize when listing your possibilities, stating a design is HV is stating that it only has these two symmetries, not any others. Actually, if a design has H and V, it automatically will have R, rotational symmetry of 180° as well. HV by itself, not possible; HVR, this is possible.
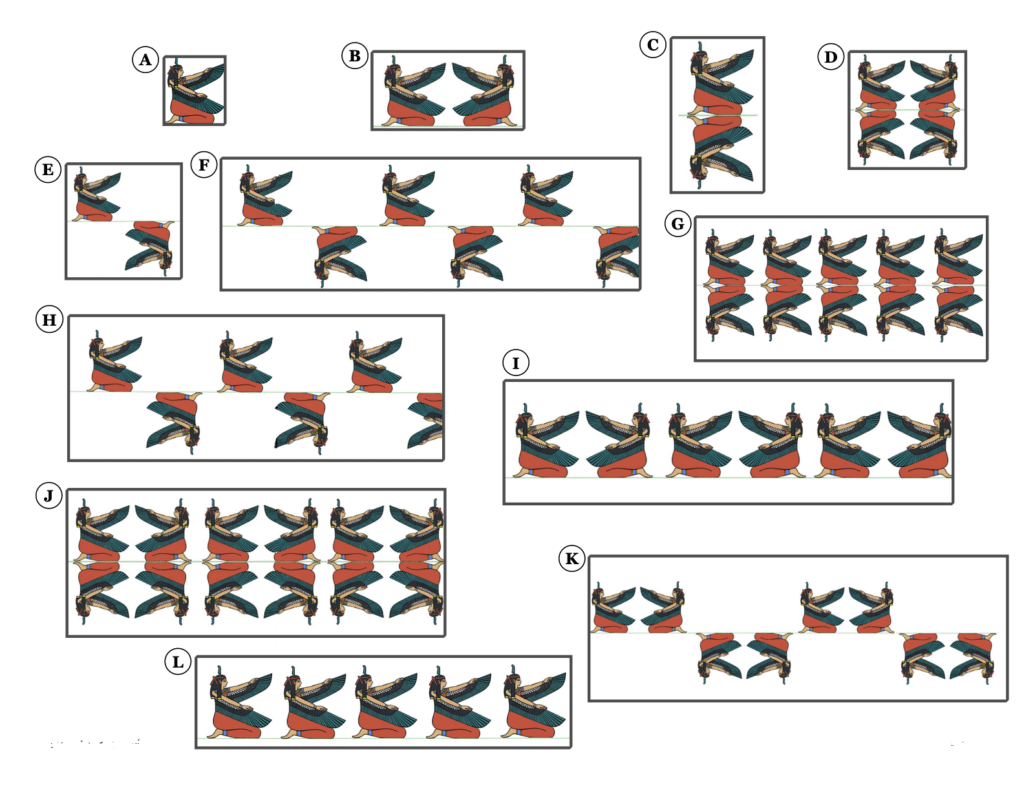
3) For each of the designs shown above, list all the symmetries that it has.
4) For each of the possibilities listed in #2), which ones are not possible? Explain why the possibilities are impossible by itself.
For example: HV is not possible because R will automatically happen as well. So HVR is possible.
5) You may have had difficulty classifying one of the designs. Which design is it and why?
6) Can you create a design that is different from the ones shown? At least one other pattern does exist. But it has the same transformation combination as one already shown. Show the possibility of one such design.
Why do you think the Egyptians excluded this pattern? Is their set of designs incomplete? Explain in a few sentences.