Problem Set A
1) Describe in words the set of points that are 5 units away from a circle with radius 5 units.
2) The measure of the supplement of an angle is 150° more than half the measure of the angle. Find the measure of the angle.
Supplementary angles will add to 180°.
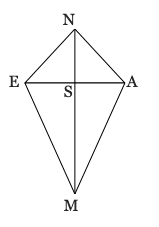
 Let the smaller angle = x
Let the smaller angle = x

3) Find the following:
a. ___________
b. ___________
c. ___________
d. ___________
e. Name all the angles that are less than 180° with vertex at point G.
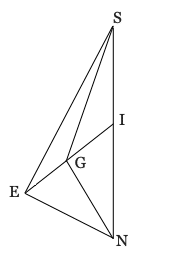
4) Given: is the ⊥ bisector of
, ∠MSA = (3x + 3y)° , SE = 6y − 5 , AE = 2x
(a bisector splits an object into 2 equal parts)
Determine the length of .
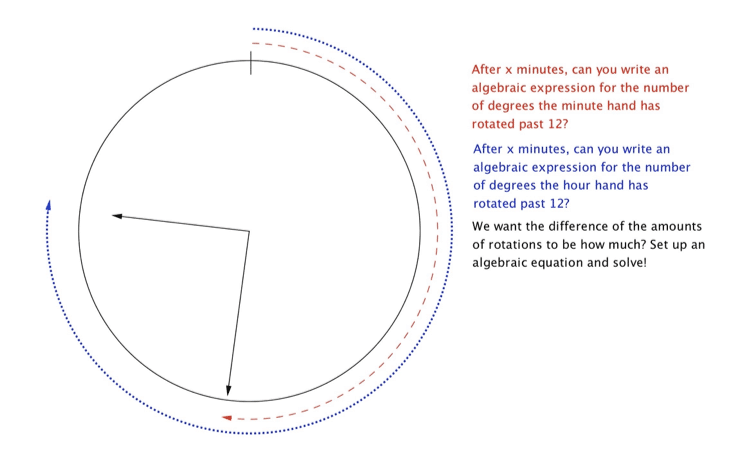
5) Find the measure of the (smaller) angle formed by the hands of a clock at 12:45.
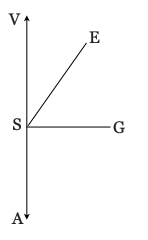
6) Given: ⊥
, ∠ESG = (8x + 5)° , ∠VSE = (x 2 + 20)°
Prove: bisects ∠VSG
Give a reason for your initial equation, do the algebraic work, and give a reason for your concluding statement.
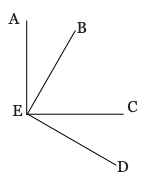
7) Given:
∠AEB = (10x + 2y)° ,
∠BEC = (12x − 4y)° ,
∠CED = (8x − 6y)°
Find the measure of ∠BEC.
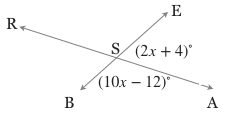
8) Given: Diagram as shown
Find: m∠BSE + m∠ASR
9) Draw and describe a picture to represent the set of all points that are equidistant from two parallel lines.
10) Rotate quadrilateral BART 90° counter-clockwise about point R.
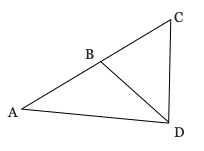
11)
Given:
bisects
AB = 4y − 7 , BC = 2y + 5
Find the length of .
12) State all symmetries in each figure.
a. 
b. 
Problem Set B
13)
Given:
, ∠ABE = (18x − 2y)° ,
∠EBD = (-6y)° , ∠DBL = (9x)°
Find: m∠EBD
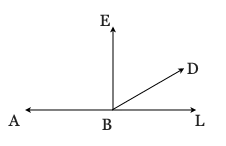
14) Determine the smaller angle made by the hands of a clock at 4:10.
15) On a graph, Point A is at (0,4). Point A is then rotated 90° clockwise about the origin to point A’. What are the coordinates of point A’ ?
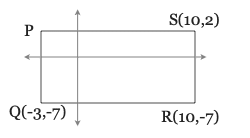
16) PQRS is a rectangle.
a) Find the coordinates of Point P.
b) Find the area of the rectangle.
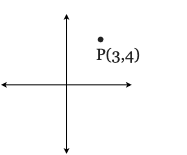
17)
a. Point P is reflected over the y-axis to point A. Find the coordinates of A.
b. Point P is reflected over the origin to point B. Find the coordinates of B.
c. If C is the midpoint of , find the coordinates of C.
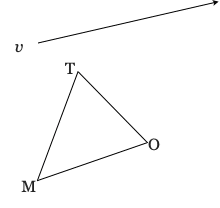
18) Use a ruler to translate ∆TOM by vector v.
19) Use a ruler, compass, and protractor to rotate figure TRAP clockwise 270º around point S.
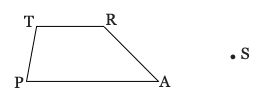
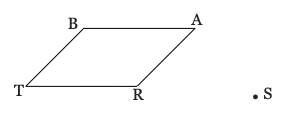
20) Rotate quadrilateral BART counter-clockwise 120º around point S. Label the image appropriately.
21) a. How many angles are in the diagram?
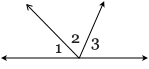
b. If the measures of of ∠1, ∠2, and ∠3 are in the ratio of 4 : 5 : 6, what is the measure of the largest angle?
Problem Set C
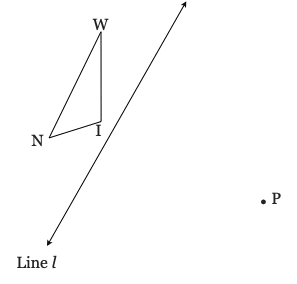
22) Use a ruler, compass, and protractor to reflect ∆WIN over line l and then rotate image ∆W’I’N’ 90° counter-clockwise about point P.
23) Translate ∆DOG by vector v and then reflect the image over line s. Label the image appropriately.
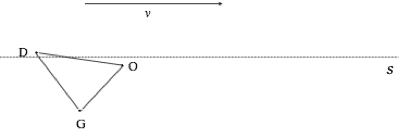
24) In problems #22 and #23, are either pair of transformations commutative? That is, if you switched the order of the operations would the result be the same?
25) At 9:00 the hands of a clock form an angle of 90°. To the nearest second, at what time will the hands of the clock next form a 90° angle?