What makes these pictures pleasing to look at?
(Well, maybe you don’t think that they are nice to look at. Everyone has their own taste. And if that’s the case, what makes these pictures look pleasing to me?)
I would note the different types of symmetry in each picture. From ancient mandalas, objects in nature, to architecture, societies have been drawn to objects that have some sort of geometric symmetry in them. Some are simple while others have a combination of several different symmetries. We will try to understand these symmetries that we see everyday.
With all types of symmetry, there is some correspondence of points so that each point can be matched to another point by following the same rule (or rules).
Or another way to think about this idea: an object is symmetric if the image “looks identical” to the original object after performing some sort of transformation.
One type of symmetry is called line symmetry. An object has line symmetry if a line can be drawn dividing the object into two mirror images of each other. Or we could say, each point has a corresponding point on the opposite side of the line that is the same distance to the line of symmetry. Depending on the orientation of the figure, we could classify different types of line symmetry into horizontal symmetry, vertical symmetry, and oblique symmetry. (Oblique is a really fancy term for not horizontal or vertical, i.e. diagonal)
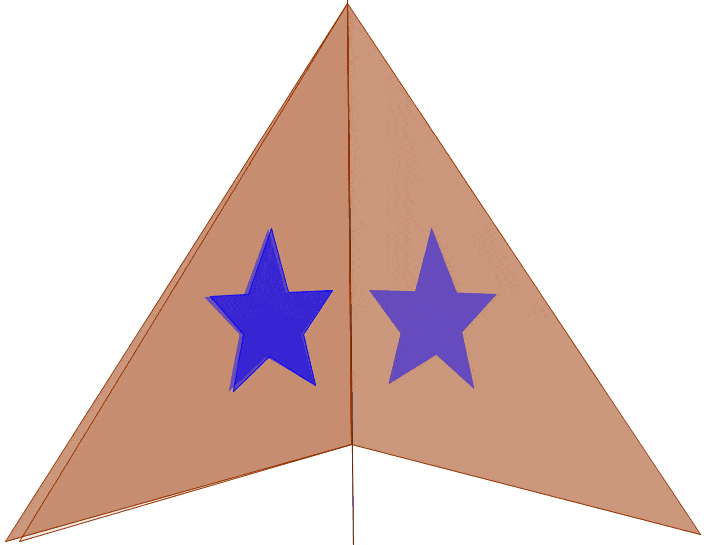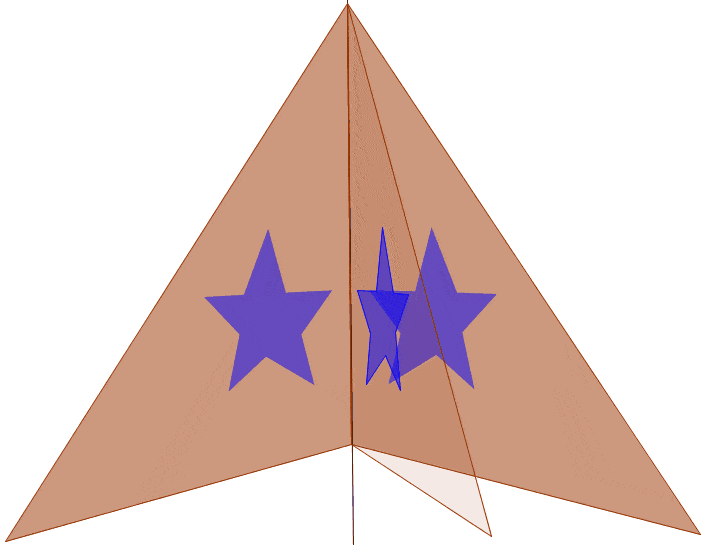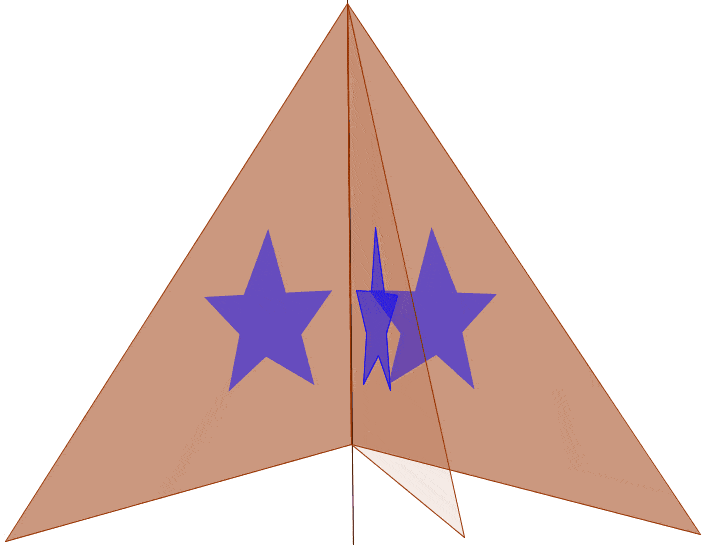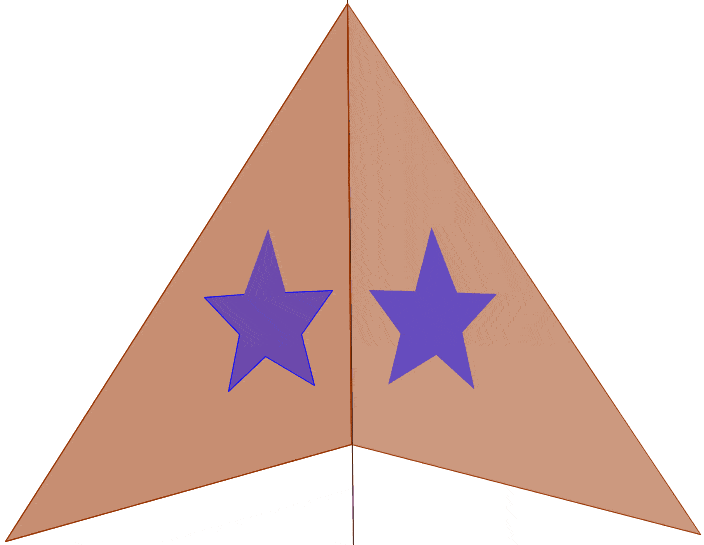
Note: the regular pentagon also has oblique symmetry.
5 lines of symmetry
Note: Saying that a figure has horizontal or vertical symmetry is dependent on the orientation of the figure. The blue figure does not have horizontal symmetry unless oriented properly.
Studies have shown that celebrities who are considered beautiful have faces which are more symmetric than people with less symmetric faces. (Tap on Giselle Bundschen’s image to test her facial symmetry)
Instead of defining point symmetry straight away, I’m going to let you deduce the meaning.
Here are some examples and counter-examples of point symmetry:
Point Symmetric
Non−Point Symmetric
So, do you think you have an idea of the meaning of point symmetry? Let’s test it out…
Tap on the card that has point symmetry:
Correct! This card is point symmetric!
Sorry! This card is not point symmetric. Try again.
Sorry! This card is not point symmetric. Try again.
If a figure can be turned 180° , or upside-down, so that it looks identical to the original figure, then the figure has point symmetry.
Imagine the letter “S”. The letter S can be rotated 180° about its center and then the new image would look identical to the original.
S
Another type of symmetry is called rotational symmetry. With this type of symmetry, if the object is turned or rotated around a central point, then the resulting image would look identical to the original. The symmetry is named by stating the number of degrees the figure would need to be turned in order to match with itself.
Another type of symmetry is called rotational symmetry. With this type of symmetry, if the object is turned or rotated around a central point, then the resulting image would look identical to the original. The symmetry is named by stating the number of degrees the figure would need to be turned in order to match with itself.
So for the figure shown in Interactive 1.1A to the left, we would say that it has 120° symmetry. There are 3 sectors of the figure, so 360° / 3 = 120° .
The snowflake figure is a little more complicated. By counting the number of points on the snowflake, 6, we would think, 360°/6 = 60°, so 60° symmetry. But what if someone else thought, “I could rotate the figure 180° and it would look the same,” and someone else might think that it is like the above example, so it has 120° symmetry. If the figure is rotated any of these degree measures, it would look identical to the original. But for simplicity, we take the lowest number because all the other values are multiples of the lowest amount. The figure could be rotated 60°, 120°, 180°, 240°, 300°, 360°, even 420°, 480° and so on, so instead of listing all the values (which would take forever), we just take the lowest number.
For the snowflake picture, some people may also state that it has point symmetry, others would think that it is not necessary to state point symmetry because by saying 60° rotational symmetry, you are also including all multiples of 60° , namely 180° . The first person would argue, “I’m just being more clear and descriptive by saying 60° rotational symmetry and point symmetry.” The second would bicker, “You are being redundant by also saying point symmetry.” Neither is more correct, just different.
Point symmetry is just a specific case of rotational symmetry (namely 180°).
Another type of symmetry that we commonly see is called translational symmetry. With translational symmetry, a figure can be moved in a particular direction by a certain distance and it will look identical to the original.
To create a figure with translational symmetry, you can imagine taking a rubber stamp and stamping along the paper in the same direction and same distance. This type is a little different because a figure that has translational symmetry can be infinite in length.
The red arrow is called a vector. It determines the direction and distance the figure is moved to be identical to the original.
Realize that this pattern should continue forever in order to be truly symmetric. But that would require a lot of stamping. If you want to continue stamping on your own, go ahead. Just let me know when you are done.
Another example of translational symmetry…
Another brick in the wall. (how can you have any pudding if you don’t eat your meat?)
(that’s a more obscure pop reference. Ask a parental unit about Pink Floyd “The Wall”)
Think about it…
Both of the patterns below have more than just translational symmetry. Can you determine what other types of symmetry they have? Tap on each to view answers.
This figure has translational symmetry and vertical line symmetry.
This figure has translational symmetry and horizontal line symmetry.
Mental Review: Ask yourself the meaning of each of the terms below. If you are unsure about any, look back in this section to reread the definition. You should be able to explain them in words to a friend and also draw examples of each.
| Symmetry | Line/Reflectional Symmetry |
| Horizontal Symmetry | Rotational Symmetry |
| Vertical Symmetry | Point Symmetry |
| Oblique Symmetry | Translational Symmetry |
For each of the symmetry questions in the interactive below, check all boxes that correctly describe the figure’s symmetry.
Answer the Section 1.1 Problems for further practice. You should complete all of these problems by downloading a pdf and writing with your tablet or on a separate sheet of paper. Be sure to show sufficient work, or provide a written explanation to show your thought process. Being able to clearly communicate your mathematical thinking is just as important as the thinking itself!
