Extra Practice Problems
Problem Set A
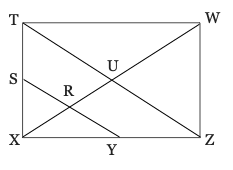
1) Review of terms. Fill in the blanks using the diagram at right.
a. 
, _________ , and ___________ all describe the same line.
b. 
and ___________ describe the same segment.
c. 
and ___________ both describe the same ray.
d. The number of angles at point R is ____________. Name all of those angles.
2)
a. Imagine a dog tied to a post in the middle of a yard. If the leash is 5 ft long, describe the set of points that the dog can walk on.
b. Imagine two towns that wish to build an airport for both towns to use. Describe the set of points where the towns could build the airport so that each town is equally distant to the airport.
3) Snoop decides that he wants to give his dog more room to run. So instead of just attaching his dog to a post, he puts up two posts and connects them with a wire. He attaches a 8 ft leash to the wire so the dog can run the full length of the wire and around on the ends. As best as possible, describe the locus of points that Snoop’s dog can run.
4) Draw and describe the locus of points in a plane equidistant from:
a) a single point.
b) two points.
c) a line.
d) a segment.
e) a ray.
f) two rays that have the same endpoint.
5) Draw a number line and label points P, R, T, and S with coordinates -4, 0.5, 1, and 6 respectively. One of these points is the midpoint (the halfway point) between two others. Which is it? Explain your reasoning to support your answer.
6) In ∆ABC, the length of 
is equal to the length of 
. The length of 
is 4 less than twice the length of . If the perimeter of ∆ABC is 52, find the length of segment .
7) Draw a labeled diagram with segments and points such that 
.
8)
a) If the minute hand of a circular clock moves 45°, how many minutes have passed?
b) If the hour hand of a circular clock moves 45°, how many minutes have passed?
Problem Set B
9) a) 
______
b) 
______
c) 
_______
d) 
_______
e) 
_______
f) 
_______
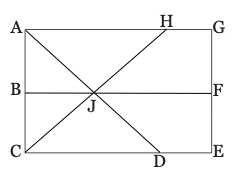
10) Given: ∠HML is a right angle, ∠HME is a right angle, ∠HMO is 3 less than 4 times ∠OML
a) Find the measure of ∠OML.
b) Find the measure of ∠EMO.
∠HMO is dependent on ∠OML, so let ∠OML = x ![\[\\]](https://geometryenjoychallenge.com/wp-content/ql-cache/quicklatex.com-c5e2793ddb59042512bf47be85fd806e_l3.svg "Rendered by QuickLaTeX.com")
11) Find the measure of the angle formed by the hands of a clock at:
a) 3:00
b) 4:00
c) 7:30
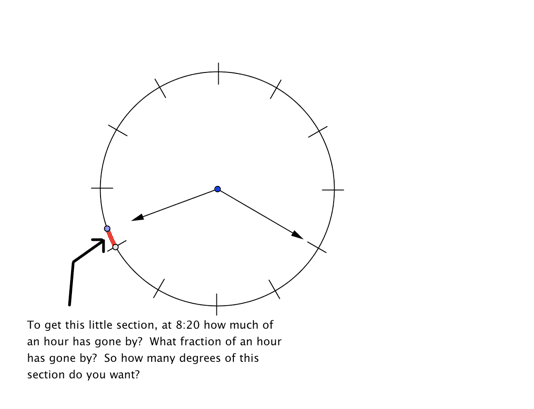
d) 8:20
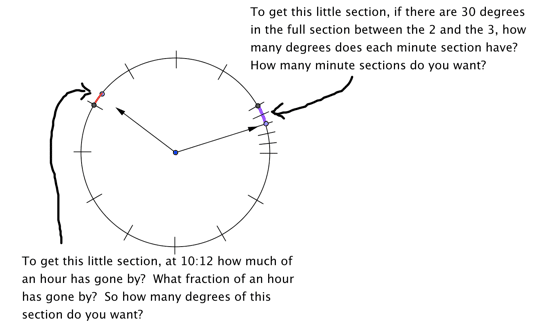
challenge! e) 10:12
12) Find the measure of ∠ABC.
(hint: you’ll need a system of two equations)
13) Draw and describe (in words) the locus of points for each:
a) All points equally distant from the two rays of an angle
b) All points 3 cm from a given line
Problem Set C
14) Draw a diagram in which the intersection of ∠GUD and ∠JOB is 
.
15)
a. What percentage of the triangles shown have 
as a side?
b. What percentage of the triangles shown have 
as a side?
