And while we’re at it, what’s a line, a ray, an angle, a locus of points, a segment, … ?
And that’s the whole problem, we can’t really represent a point. As soon as we try to draw a point, usually with a dot, we’ve already made the point too big. A point has no dimension and no size.
A point is a location or position on a plane.
So when we draw a point on paper, we are just referring to that position on the plane.
So, what’s the plane?
Uh-oh, I’ve already used a word, namely “plane”, that I haven’t clearly defined yet to explain the word “point”. How can we know the meaning of these terms if they use undefined terms? Euclid had this same problem thousands of years ago when he started geometry. (Now you can say you have something in common with Euclid, possibly the greatest mathematician ever.)
Undefined Terms are words that we can’t really clearly define, but generally we all understand what it is that we are trying to describe.
A plane is an infinitely large flat surface with no thickness.
We try to represent planes by drawing something that looks like ![]() . But we have to realize that the plane doesn’t stop, it has no edges, and it also has no thickness. Sometimes people will use a piece of paper to represent a plane, which is fine if you imagine an infinitely large piece of paper with no thickness.
. But we have to realize that the plane doesn’t stop, it has no edges, and it also has no thickness. Sometimes people will use a piece of paper to represent a plane, which is fine if you imagine an infinitely large piece of paper with no thickness.
Now, you might be thinking, “Hey, you skipped something.” A point has no dimension because it doesn’t extend in any direction. A plane is two dimensional because it extends in two directions (either left/right and up/down, or horizontally and vertically, or north/south and east/west).
What is a one dimensional object? Something that extends forever in just one direction, infinitely horizontal? Or just vertical. Make a guess…. Go ahead, I’ll wait. [Game show music here]
[Scroll down after you have answered]
A line is the set of points, infinitely in opposite directions, with no width.
We could also describe a line as all the points from one point, A, directly straight to another point, B, and continuing in that same direction forever; and all the points from point B to point A continuing in that same direction forever. Probably, you’ve worked with the number line; that’s a great example of a line.
So, I’ve tried to explain a point, a line, and a plane. You might do some research on your own, or read somewhere else, and find different definitions. These aren’t called undefined terms for nothin’. Nevertheless, we are trying to describe the same objects. They’re just undefinable. And these are all theoretical objects; we can’t actually draw a point, or a line, or a plane. If we did, it would be too thick. But we all can generally understand what is being described. Or at least I hope we can.
Remember when you played connect-the-dots? You’d see two points and you’d connect them by drawing a segment from one point to another. You were making a segment.
A segment is the set of all points on a line directly between two points.
What does a segment have that a line doesn’t have? Well, a couple of things. Mainly, it has two endpoints. A segment has definitive ends; therefore, it has a definite length. We could measure the length of a segment and say, “Segment AB with length 4 cm.” Or as an equation, = 4 cm. Whereas with a line, what is its length? It has infinite length.

Finally, what if there were a line-segment hybrid? A half line, half segment? A set of points that had one endpoint but went infinitely in just one direction? That is called a ray.
A ray is a portion of a line that starts at one endpoint and extends infinitely in one direction.

Points, Lines, Segments, and Rays. These are the basic building blocks of geometry. All of these are considered sets of points. But we could imagine lots of other sets of points. Sets of points that satisfy different conditions are called a locus of points. Let’s imagine some different locus of points.
Think about it…
The locus of points that are exactly 3.5 cm from a given point is a circle. The actual points of the circle are just the points that define the “edge” of the circle. The circle does not include all the points within.
The locus of points that are less than 3.5 cm from a given point are all points within a circle, but not including the circle itself.
Can you think of a real life analogy to each of these locus of points using a dog in a yard?

We can also think about two different sets of points and asking if these sets of points share any points; do they have any points in common? Or we can think about taking the sets of points and putting them together; what is the set of points if we combine both sets of points?
These two actions are called the intersection and union of points.
![]() is the symbol for intersection; it can also have the meaning of “and”. For the statement A
is the symbol for intersection; it can also have the meaning of “and”. For the statement A B, you are thinking, “What set consists of the elements that are in both set A and in set B ?”
![]() is the symbol for union; it can also have the meaning “or”. For the statement A
is the symbol for union; it can also have the meaning “or”. For the statement A B, you are thinking, “What set consists of all points that are in set A or in set B?” Also, “What is the resulting set if I combine all of these elements in set A with the elements in set B ?”
Examples: Tap on each equation to see an explanation.
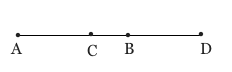
Intersection Example:
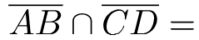
 What points are on
What points are on
Union Example:
 What points are on segment
What points are on segment
In the following set of questions for you to try, tap on the diagram below and answer each by dragging the correct answer which corresponds to the correct set of points.
Perhaps you noticed I snuck a new term in those set of problems.
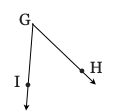
(read aloud as “angle IGH” or “angle HGI”).
An angle is the union of two rays that share the same endpoint.
Because an angle is made up of rays, we can’t really measure its length because the rays go on for ever. Instead, we measure the space “between” the two rays.
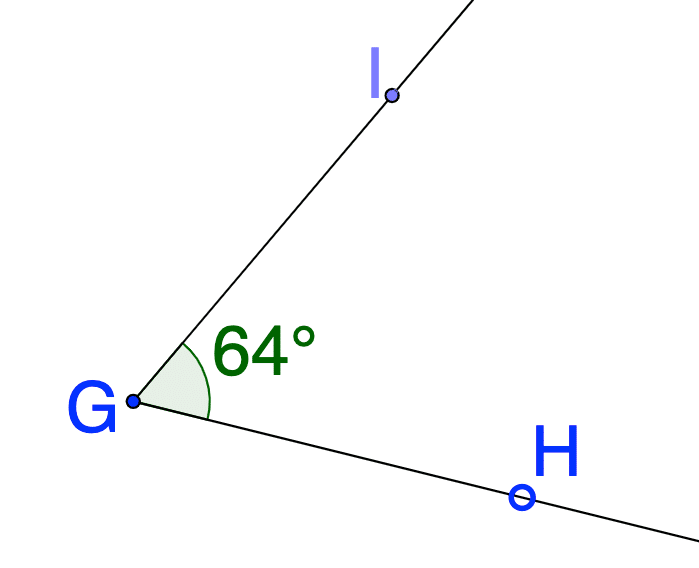
We can classify these angles by their measure:
Acute angles have a measure that is between 0° and 90° .
Right angles have a measure that is equal to 90° . (These are marked with a little square in the angle).
Obtuse angles have a measure between 90° and 180° .
And Straight angles have a measure that is equal to 180° .
Right angles and straight angle are special ones to mention.
If two rays form a right angle, we say that the rays are perpendicular. (Note: ⊥ means perpendicular)
Or we could say, if two rays are perpendicular, then they form right angles.
Straight angles are special because the rays are opposite rays. It looks like a line! In fact, the set of points that make up the line are the same set of points that make up the straight angle.
Think about it…
What are all the ways that you can name the set of points shown? Tap the line to see all possible answers.


Imagine Tweedle-Dee and Tweedle-Dum looking at the diagram above and have the following conversation:

T.-Dee: “∠QRP is a straight angle, so it is equal to 180°.”
T.-Dum: “Well, how do you know? Maybe it’s 179.82°. Or maybe it’s 180.001°. How do you know that it’s 180°?”
They could argue about this situation forever. So, we have to come to some sort of agreement about straight angles. Let’s just say, “If it looks straight, it is straight.” We’ll say that the intention of the diagram making a straight line actually is a straight line. So, this is the only measurement in a diagram you are allowed to assume.
All right, I’ve introduced a lot of terms in this section but I hope that you have heard many of these terms and perhaps already knew the meanings of many. Look through the list below and mentally ask yourself the meaning of each. Then work through the set of problems for practice.
| Point | Union |
| Plane | Intersection |
| Line | Angle |
| Segment | Acute Angle |
| Ray | Right Angle |
| Endpoints | Obtuse Angle |
| Locus of Points | Straight Angle |
| Circle | Perpendicular |