Transformations by Hand
And because you’ve been so good in following along, I’ll even let you choose which hand.
Sure any graphic designer worth their salt is a master at transforming figures on their computer. Computers were huge time savers for graphic designers; just a click to reflect or rotate. And if they messed up, Undo!
But they all started working by hand. You’ve got to feel it.
Before you continue, take the short quiz below to see if you understand the information needed for each type of transformation.
You will either need to print out the next few pages or make a sketch of the picture on your own paper.
Use a ruler and protractor to be as accurate as possible! Don’t try to transform the entire triangle at once. Instead, just transform one vertex to find the image point, then transform another vertex, then the last; then connect the image points to form the new triangle.
1. Given ∆ABC and vector v. Translate ∆ABC by vector v and properly label ∆A’B’C.
2. Given ∆DEF and line l. Reflect ∆DEF over line l and properly label ∆D’E’F’.
3. Given ∆JKL and central point X. Rotate ∆JKL 180° about point X and properly label ∆J’K’L’. You should be able to do this without a protractor if you are slick.
Point X may be a bit large for a point, but don’t judge.
4. Given ∆GHI and central point I. Rotate ∆GHI 120° clockwise about point I and properly label ∆G’H’I’.
5. Given ∆MNO and center of dilation point Y. Dilate ∆MNO by a factor of 2 from point Y and properly label ∆M’N’O’.
To dilate a point with a positive scale factor, the image point would move in the direction of the ray from the center of dilation to the pre-image.
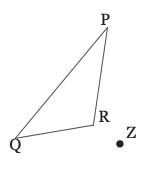
6. Given ∆PQR and center of dilation point Z. Dilate ∆PQR by a factor of -1 from point Z and properly label ∆P’Q’R’.
To dilate a point with a negative scale factor, the image point will move in the opposite direction of the ray from the center of dilation to the pre-image.
